BOJ 2263 - 트리의 순회 [Divide & Conquer]
BOJ 2263 - 트리의 순회 Gold Ⅱ
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
✨ PreOrder, PostOrder, InOrder란?
전위 순회, 후위 순회, 중위 순회이다.
이는 Tree에서의 traversal인데, 전위는 노드 왼쪽에서 방문하고, 중위는 노드 아래에서 만나고, 후위는 노드 오른쪽에서 만난다.
이를 그림으로 보면 이해하기 쉽다.
1️⃣ PreOrder Traversal
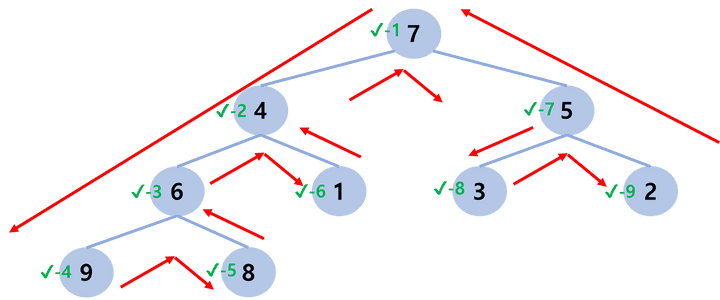
2️⃣ InOrder Traversal
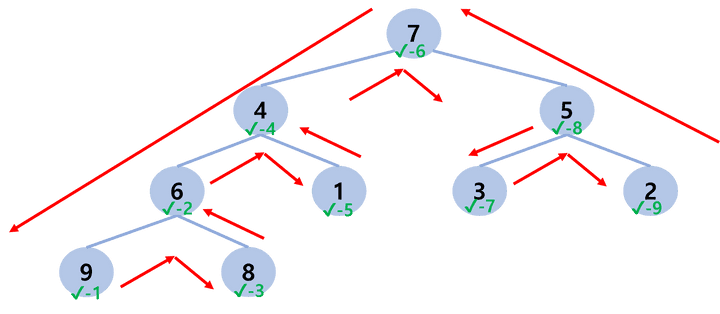
1️⃣ PostOrder Traversal
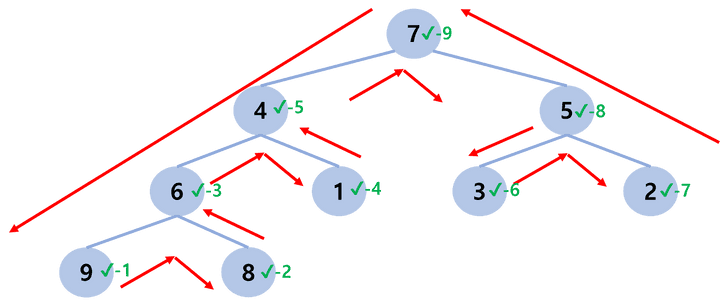
위 Tree에서의 순서
| InOrder | 9 | 6 | 8 | 4 | 1 | 7 | 3 | 5 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| PostOrder | 9 | 8 | 6 | 1 | 4 | 3 | 2 | 5 | 7 |
How to Solve?
💥 PostOrder의 특징과 InOrder의 특징을 활용하자!
PostOrder 순서의 경우 Root 노드를 맨 마지막에 방문하는 것을 알 수 있습니다.
InOrder 순서의 경우 Root 노드를 기준으로 왼쪽은 Left SubTree가 되고, 오른쪽은 Right Sub Tree 가 됩니다.
이 두 사실을 활용해서 Left SubTree 와 Right SubTree로 분할하며 해결한다면 해결할 수 있습니다.
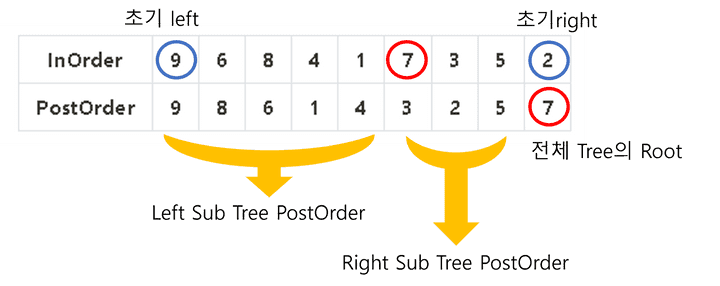
위 그림과 같이 post order에서 현재 Tree에서 Root를 뽑아내고 InOrder 정보를 통해 왼쪽 서브 트리의 노드 개수, 오른쪽 서브 트리의 노드 개수를 구한다.
우리는 PreOrder Traversal을 할 것이기 때문에 왼쪽 서브 트리부터 재귀적으로 다시 나누면서 자기 자신의 노드만 남을 때 까지 진행한다.
💥 종합적으로 그림으로 살펴보겠습니다.
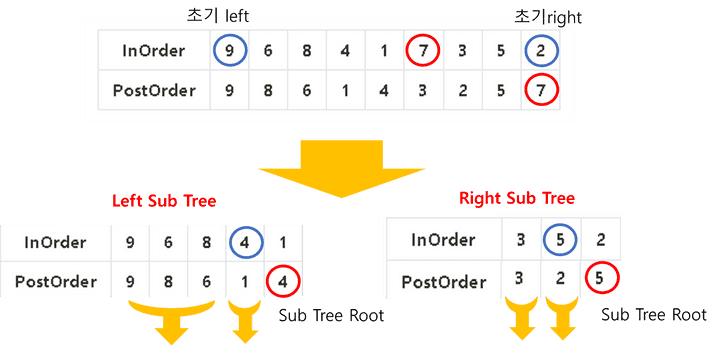
위 그림과 같이 진행하면서 자기 자신 노드만 남을 떄까지 진행합니다.
또한, 현재 Tree에서 PostOrder 정보를 통해 얻은 Root 는 바로 출력에 추가시켜준다면 왼쪽 서브 트리로 divide하면서 진행하기 때문에 자연스럽게 PreOrder Traversal을 진행할 수 있습니다.
✨ Java Code
package com.day0809;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class BOJ_2263 {
static List<Integer> inOrder; // in-order traversal
static StringBuilder sb;
// Left Sub Tree & Right Sub Tree 분리한다.
static void solve(int inLeft, int inRight, List<Integer> post) {
// inLeft > inRight 시 종료
if (inLeft > inRight ) return;
if (inLeft == inRight) { // 왼쪽으로 쭉 가다가 하나만 남았다면 더 이상 왼쪽으로 갈 자식이 없다 -> 출력 후 종료
sb.append(post.get(0) + " ");
return;
}
// 현재 Sub Tree 중 Root는 post 에서 마지막에 방문된 노드이다.
int subRoot = post.get(post.size() -1 );
// 서브트리의 root는 바로 방문 -> 출력한다.
sb.append(subRoot + " ");
// in-order traversal 에서 방문된 순서를 찾아서 그 index를 기준으로 왼쪽은 Left Sub Tree - 오른쪽은 Right Sub Tree
int idx = inOrder.indexOf(subRoot);
solve(inLeft, idx-1, post.subList(0, idx - inLeft)); // 왼쪽 서브 트리 탐색
solve(idx+1, inRight, post.subList(idx-inLeft, post.size() - 1)); // 오른쪽 서브 트리 탐색
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
inOrder = new ArrayList<>();
List<Integer> postOrder = new ArrayList<>();
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
inOrder.add(Integer.parseInt(st.nextToken()));
}
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
postOrder.add(Integer.parseInt(st.nextToken()));
}
solve(0, N-1, postOrder);
System.out.println(sb);
}
}
💥 끝!!
✨ 잘못된 부분은 많은 조언 및 지적 부탁드립니다. - JunHyxxn