BOJ 2632 - 피자 판매 Gold Ⅱ

BOJ 2632 - 피자 판매

문제

고객이 두 종류의 피자 A와 B를 취급하는 피자가게에서 피자를 주문하고자 한다.
<그림 1>과 같이 각 종류의 피자는 다양한 크기의 여러 개의 피자조각으로 나누어져 있다.
각 조각에 쓰여진 숫자는 피자조각의 크기를 나타낸다.

고객이 원하는 피자의 크기를 이야기하면, 피자가게에서는 한 종류의 피자를 2 조각 이상 판매할 때는 반드시 연속된 조각들을 잘라서 판매한다.
이때 판매한 피자조각의 크기 합이 주문한 크기가 되어야 한다. 판매한 피자조각은 모두 A종류이거나, 모두 B종류이거나, 또는 A와 B 종류가 혼합될 수 있다.
예를 들어서, <그림 1> 과 같이 잘라진 피자가 있을 때, 손님이 전체 크기가 7 인 피자를 주문하면, 피자 가게에서는 <그림2>와 같이 5 가지 방법으로 피자를 판매할 수 있다.

피자가게에서 손님이 원하는 크기의 피자를 판매하는 모든 방법의 가지 수를 계산하는 프로그램을 작성하시오

입력

첫 번째 줄에는 손님이 구매하고자 하는 피자크기를 나타내는 2,000,000 이하의 자연수가 주어진다.
두 번째 줄에는 A, B 피자의 피자조각의 개수를 나타내 는 정수 m, n 이 차례로 주어진다 (3 ≤ m, n ≤ 1000).
세 번째 줄부터 차례로 m 개의 줄에는 피자 A의 미리 잘라진 피자조각의 크기를 나타내는 정수가 주어진다.
그 다음 n 개의 줄에는 차례로 피자B의 미리 잘라진 피자조각의 크기를 나타내는 정수가 주어진다.
각 종류의 피자조각의 크기는 시계방향으로 차례로 주어지며, 각 피자 조각의 크기는 1000 이하의 자연수이다.

출력

첫째 줄에는 피자를 판매하는 방법의 가지 수를 나타내는 정수를 출력한다. 피자를 판매하는 방법이 없는 경우에는 숫자 0을 출력한다.

🍺 How to Solve?

예제와 같이 피자A는 5조각으로 2, 2, 1, 7, 2 로 이루어져있다고 한다.

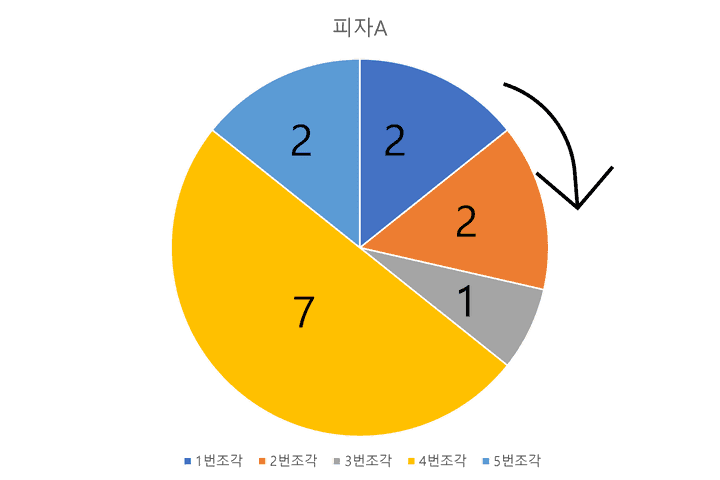
이 피자에서 사용 가능한 조각의 조합은 1조각, 2조각, 3조각, 4조각, 5조각 인 경우이다.
피자가 반드시 이어져야 하기 때문에 어느 피자 조각에서 시작하느냐에 따라 다른 값이다.

피자를 조금 확장해서 생각해본다.

1️⃣ 조각인 경우 : {2}, {2}, {1}, {7}, {2}
2️⃣ 조각인 경우 : {2, 2}, {2, 1}, {1, 7}, {7, 2}, {2, 2}
3️⃣ 조각인 경우 : {2, 2, 1}, {2, 1, 7}, {1, 7, 2}, {7, 2, 2}, {2, 2, 2}
4️⃣ 조각인 경우 : {2, 2, 1, 7}, {2, 1, 7, 2}, {1, 7, 2, 2}, {7, 2, 2, 2}, {2, 2, 2, 1}
5️⃣ 조각인 경우 : {2, 2, 1, 7, 2} 🟥 => 5조각은 어느 위치에서 시작해도 상관없이 똑같다.

위와 같은 결과가 나온다.

위 결과들은 어느 위치에서 시작해 몇 번 조각까지인지에 해당하는 누적합으로 구할 수 있다.
누적합은 DP와 Segment Tree로 구현할 수 있는데, 사실 이 문제는 값이 변경되지 않기 때문에 DP로 구현하는 것이 훨씬 쉽다.
하지만, 학습을 위해 Segment Tree로 구현했습니다.

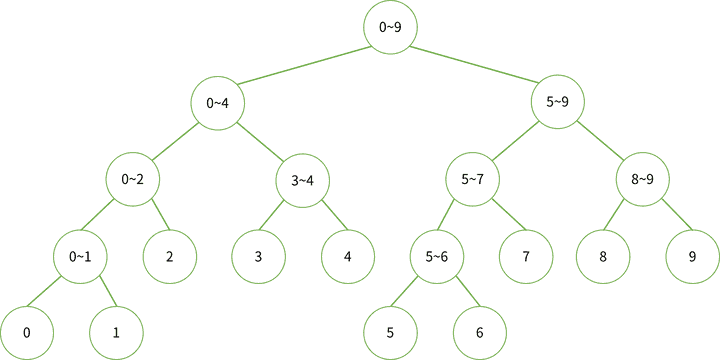
2, 2, 1, 7, 2 까지이지만 5번조각 이후에 다시 1번조각으로 돌아오기 때문에 편의를 위해 이 5조각을 붙여 10조각으로 설정하고 Segment Tree를 설정합니다.

Segment Tree의 특성 상 Leaf Node가 N이라면 Internal Node는 항상 N-1 이 됩니다.
다만 우린 5조각이 아닌 그 2배 10조각을 사용했기 때문에, $Leaf Node = 2*N$ , $Internal Node = 2*N - 1$ 이 된다.
총 node의 수는 $4*N - 1$ 개 이다.

🎯 Segment Tree의 높이

h = $\lceil$log_2{4*N - 1}$\rceil$

✨ Java - Binary logarithm

$log_{2}{x} = log_{10}{x} / log_{10}{2}$

아래 코드는 본 소스 코드에서 사용한 코드입니다. 높이를 구하기 위해서는 올림이 필요해 해당 로직까지 적용했습니다.

static int base2log(int n) {
		return (int)Math.ceil(Math.log10(n) / Math.log10(2));
}

🔥 Key Idea

Segment Tree를 이용해 구간합 데이터를 만들었다면, 각 피자로 만들 수 있는 크기에 대해 총 몇가지 경우의 수가 나오는지 저장하는 배열을 생성합니다.
이는 1조각일 경우부터 N-1 조각일 때 까지 -> {1}, {2}, … , {1,2,…,N-1}, {N,1,2,…N-2} 까지 구간합들을 조회해 가능한 크기별 가능 횟수를 저장합니다.

문제의 Test Case에 적용한다면
Pizza A 는 2,2,1,7,2 => 0~14 크기만큼 가능하다.
Pizza B 는 6, 8, 3 => 0~17 크기만큼 가능하다.

주의할 점은 두 피자 모두 0인 경우가 1개씩 존재하고, 모두 사용하는 최대 크기의 경우는 1개 존재한다.

피자 A와 피자 B의 크기에 대한 가능한 조각의 개수 배열은 길이가 서로 다르고
우리가 구하고자 하는 피자의 크기(P)를 구하기 위해서는 피자 A에서 i만큼 가져온다면 피자 B에서는 P-i 만큼 가져오면 된다.

이를 잘 고려해서 계산한다면 정답을 구할 수 있습니다.

🔑 Time Complexity

Segment Tree를 만들기 위해서 $O(NlogN + MlogM)$
크기별 가능한 조각 조합 개수 배열 구하기 위해 $O(N^2 + M^2)$
피자 크기 P를 만들기 위해 $O(P/2)$

총 약 $O(N^2)$ 만큼 소요된다.

✨ Java Code

public class BOJ_2632_피자판매 {
	static int order, N, A, B, M;
	static int[] nums, tree;
	public static void main(String[] args) throws IOException{
		BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		order = Integer.parseInt(br.readLine());

		st = new StringTokenizer(br.readLine());
		A = Integer.parseInt(st.nextToken());
		B = Integer.parseInt(st.nextToken());

		nums = new int[A];
		M = A;
		N = 1<<base2log(4*A-1);
		tree = new int[N];
		int totalA = 0;
		for (int i = 0; i < A; i++) {
			nums[i] = Integer.parseInt(br.readLine());
			totalA += nums[i];
		}
		initSegmentTree(1, 0, 2*A-1);

		int[] posA = new int[totalA+1];
		posA[0] = 1;
		posA[totalA] = 1;
		for (int i = 0; i < A-1; i++) {
			for (int j = 0; j < A; j++) {
				int sum = find(0, 2*A-1, j, j+i, 1);
				posA[sum]+=1;
			}
		}

		nums = new int[B];
		M = B;
		N = 1<<base2log(4*B-1);
		tree = new int[N];
		int totalB = 0;
		for (int i = 0; i < B; i++) {
			nums[i] = Integer.parseInt(br.readLine());
			totalB += nums[i];
		}
		initSegmentTree(1, 0, 2*B-1);
		int[] posB = new int[totalB+1];
		posB[0] = 1;
		posB[totalB] = 1;
		for (int i = 0; i < B-1; i++) {
			for (int j = 0; j < B; j++) {
				int sum = find(0, 2*B-1, j, j+i, 1);
				posB[sum]+=1;
			}
		}

		int cnt = 0;
		for (int i = 0; i <= order/2; i++) {
			if(isRange(i, posA.length) && isRange(order-i, posB.length)) {
				cnt += posA[i]*posB[order-i];
			}
			if(isRange(order-i, posA.length) && isRange(i, posB.length)) {
				if(i == order-i) continue;
				cnt += posA[order-i]*posB[i];
			}
		}
		System.out.println(cnt);
	}
	static boolean isRange(int x, int R) {
		return !(x<0 || x>=R);
	}
	static int base2log(int n) {
		return (int)Math.ceil(Math.log10(n) / Math.log10(2));
	}

	static int initSegmentTree(int node, int start, int end) {
		if(start == end) {
			tree[node] = nums[start >= M ? start-M : start];
			return nums[start >= M ? start-M : start];
		}
		int mid = (start+end)/2;
		int l_sum = initSegmentTree(node*2, start, mid);
		int r_sum = initSegmentTree(node*2+1, mid+1, end);
		return tree[node] = l_sum+r_sum;
	}
	static int find(int start, int end, int left, int right, int node) {
		if(end < left || right < start) return 0;
		if(left<= start && end <= right) return tree[node];

		int mid = (start+end)/2;
		int l_sum = find(start, mid, left, right, node*2);
		int r_sum = find(mid+1, end, left, right, node*2+1);
		return l_sum+r_sum;
	}
}

💥 끝!!

✨ 잘못된 부분은 많은 조언 및 지적 부탁드립니다. - JunHyxxn