SWEA 4111 - 무선 단속 카메라 [SWEA 문제 - Disjoint-Set, Union-Find]
SWEA 4111 - 무선 단속 카메라 D-Ⅳ
이 문제는 SWEA 문제입니다. 문제 출처 : 무선 단속 카메라
🔥 Point
이 문제의 핵심은 Kruskal 알고리즘에서 아이디어를 떠올렸다.
Kruskal 알고리즘은 MST(Minimum Spanning Tree)를 만들기 위한 알고리즘 중 하나이다.
MST란 최소 비용으로 만들 수 있는 Spanning Tree(신장 트리)를 찾는 알고리즘이다.
신장 트리란, 모든 노드를 포함하면서 사이클이 존재하지 않는 그래프를 의미한다.
즉 최소비용으로 사이클 없이 모든 노드를 포함하는 그래프를 찾는 것이다.
🌟 MST 찾기 위해서 Kruskal 알고리즘은 모든 간선 중 가장 비용이 낮은 간선들부터 제거하며 해당 간선으로 이어져 있는 노드들끼리 합쳐주는 것 이다.
이를 이 문제에 적용해 해결할 것이다.
💥 How to Solve?
수신기는 모든 카메라들을 포함하고 있어야 한다. 이를 반대로 생각해봤다. 모든 카메라에 하나의 수신기들이 배당되어 있고, 가장 붙어있는 카메라들을 하나의 수신기가 담당하도록 한다.
이해를 위해 그림으로 살펴보자.
1️⃣ 최초에는 모든 카메라에 수신기를 부여한다.
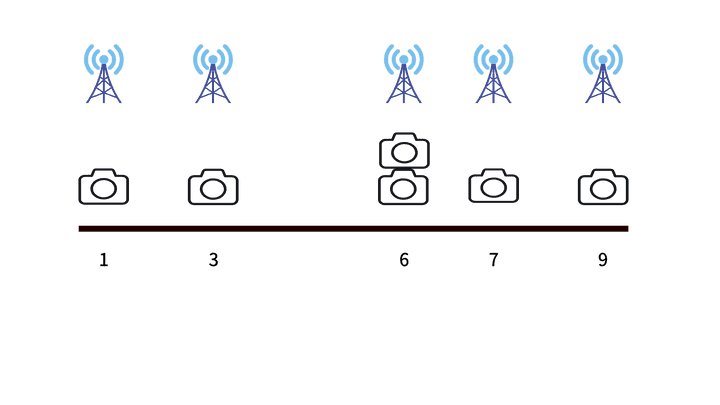
2️⃣ 카메라간 거리가 가장 짧은 6, 7 카메라에 해당하는 수신기를 하나로 Union한다.
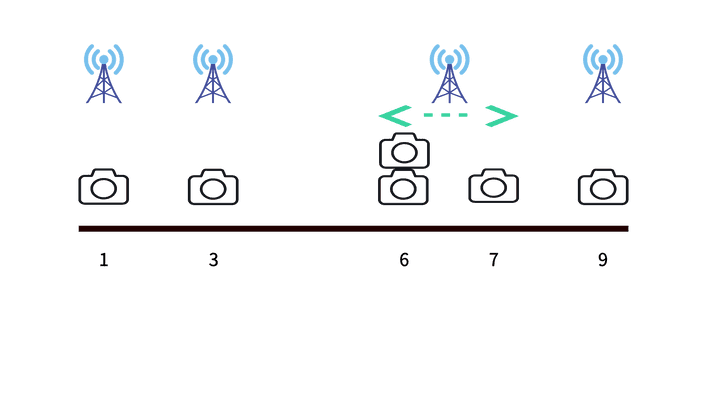
3️⃣
그 다음 거리가 짧은 1,3 카메라에 해당하는 수신기를 줄여준다.
이 때, 6-7, 9 간의 거리도 마찬가지로 2인데 둘 중 어느 것을 줄이더라도 결과는 똑같다.
결국엔 1-3, 6-7, 9 라면 거리가 총 3이 되고, 1, 3, 6-9 라면 마찬가지로 거리가 3이기 때문이다.
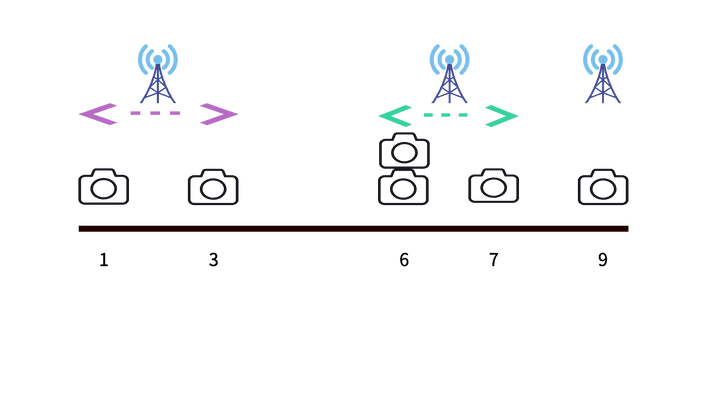
4️⃣ 문제에서 주어진 수신기는 2개이기 때문에 한 번 더 수신기를 줄여 위 그림과 같은 상태를 만들어 준다.
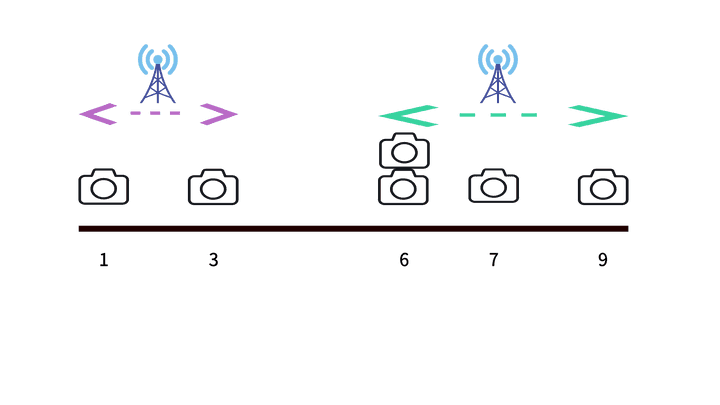
이렇게 접근한다면 수신기가 몇개가 되든 올바른 답을 구할 수 있다.
‼ 주의할 점 ‼
1️⃣ 카메라 중복된 위치는 고려하지 않아도 된다. set을 이용해 줄여주고 N도 이에 맞게 재정의해주면 된다.
2️⃣ 카메라 간 거리 구하기 위해서 정렬해줘야 한다.
3️⃣ UnionFind를 위해서 배열을 이용하게 되면 카메라의 절대위치 값이 💥1M 이기 때문에 메모리 초과가 발생한다.
3번 문제를 해결하기 위해서 배열을 사용하지 않고 dictionary를 사용한다.
✨ UnionFind 자료구조
설명하기에는 배열 형태가 더 쉽기 때문에 배열로 설명한다.
초기에는 parent가 자기자신인 배열이 생성된다. (0은 존재하지 않는 노드라 생각하면 된다.)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| parent | 0 | 1 | 0 | 3 | 0 | 0 | 6 | 7 | 0 | 9 |
여기에서 6, 7이 합쳐질 때, 더 작은 숫자를 root로 만들면 된다. 즉 7의 parent 값이 6으로 변경된다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| parent | 0 | 1 | 0 | 3 | 0 | 0 | 6 | 6 | 0 | 9 |
마찬가지로 1,3 이 Union 되면서 3의 parent값이 1로 변경되고, 9는 7과 합쳐지는데 7의 root는 6이기 때문에 6으로 변경된다. 따라서 아래와 같은 배열이 완성된다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| parent | 0 | 1 | 0 | 1 | 0 | 0 | 6 | 6 | 0 | 6 |
위와 같이 Union을 하기 위해서는 해당 노드의 parent를 찾는 Find가 필요한데 이는 간단히 자기 자신의 root를 parent에 기록하면 쉽게 해결할 수 있다.
✨ Python Code
"""
문제 출처 : https://swexpertacademy.com/main/code/problem/problemDetail.do?problemLevel=3&problemLevel=4&contestProbId=AWJHjcFqdyoDFAUH&categoryId=AWJHjcFqdyoDFAUH&categoryType=CODE&problemTitle=&orderBy=FIRST_REG_DATETIME&selectCodeLang=PYTHON&select-1=4&pageSize=10&pageIndex=10
UnionFind 을 이용해 해결할 수 있다.
"""
from collections import defaultdict
T = int(input())
def find(disjoint_set, num):
if disjoint_set[num] == num:
return num
num = disjoint_set[num]
return num
def union(disjoint_set, a, b):
a = find(disjoint_set, a)
b = find(disjoint_set, b)
if a == b:
return disjoint_set
disjoint_set[max(a, b)] = min(a, b)
return disjoint_set
for t in range(1, T+1):
N = int(input())
K = int(input())
## 중복된 카메라 위치는 고려하지 않아도 된다. set으로 줄여준다.
camera = set(map(int, input().split()))
## 정렬 해줘야 카메라간 거리 알 수 있다.
camera = list(sorted(camera))
## 중복 제거했으니 N을 다시 정의해줘야한다.
N = len(camera)
## 인접 거리를 두 카메라의 위치를 key로 잡는다.
adjacent_dist = defaultdict(int)
for i in range(len(camera)-1):
adjacent_dist[(camera[i], camera[i+1])] = camera[i+1] - camera[i]
disjoint_set = {c: c for c in camera}
adjacent_dist = list(sorted(adjacent_dist.items(), key=lambda x: x[1]))
total = 0
for info in adjacent_dist:
if N <= K:
break
N -= 1
nodes, dist = info
a, b = nodes
disjoint_set = union(disjoint_set, a, b)
total += dist
print("#{} {}".format(t, total))
💥끝!!
✨ 잘못된 부분은 많은 조언 및 지적 부탁드립니다. - JunHyxxn